Projecting a point on a Bézier curve

Hi All my readers.

In this post I'd like to show how to perform the projection of a point to rational cubic Bézier curve.

In fact, this procedure may not seem very useful for everyone. In the end, is there any sense to do Bézier curves in problems of geometric programming problems? However, if someone of the readers of this post had heard about such concepts as BSpline or NURBS, I am sure that this post will show them not only interesting but useful too.

Therefore, I will ask my readers to take my word - namely, any BSpline or NURBS-curve can be converted into one (or a series) of Bézier curves. Yes, do not be surprised. It is true. Therefore, knowing how to treat the problem with Bézier curves will always have the opportunity to consider the problems associated with BSpline or NURBS curves in a similar way.

Consider the rational Bézier curve of order 3. We will talk specifically about the Bézier curve of that order.

Rational Bézier curve of order 3 define by:

Denote a point that is projected onto this curve as G;

Next, we use one of the properties of Bézier curves: namely “the transfer of all control points of a Bézier curve by the same vector does not affect the shape of the curve" and give the origin of the system coordinates of the Bézier curve to a point G.

Thus, in view of transfer of control points of the curve, then we will use the following change of variables:

Give the equation of a Bézier curve to a polynomial form:

Make the following change of:

then the equation of a Bézier curve takes the form:

Define the derivative of this equation:

After the algebraic manipulations, we obtain the following equation:

where

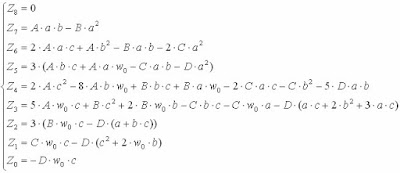
Now we can return to the equation of determining the projection of a point on a Bézier curve.
Required equation has the form:

Or:

Now we can obtain a polynomial equation, whose solution will give us the answer to the question "Where are projected onto a point on a Bézier curve?"

where:

There are many ways to solve polynomial equations. In the case of this problem I used the «Bairstow-Newton» method, which allows us to be given up to find the real and complex roots of polynomial equations. This method worked well in terms of both speed and accuracy of search results.

After receiving the results of solving polynomial equations, only one correct result from the list of solutions is necessary to choose.

To do it, consider the following factors:

1. 
   «Bairstow-Newton» method allows us to find as real as imaginary roots. Thus, the roots of polynomial equations, which contain the imaginary part, cannot be useful.
2. Since the domain of definition of a Bézier curve lies between the values [0..1], those are real roots, which are not included in this area are not correct.
3. Because of solutions of polynomial equations obtained several real roots, then choose follows the root, which corresponds to the minimum distance between a point on the Bézier curve and the projected point.
4. If resulting solutions of polynomial equations obtained several real roots, and the distance between corresponding points on the Bézier curve and the projected point are equal, then this situation should be considered as a special (exceptional). For example if the projected point on the circle from the center of this circle.
   

Also, you should noticed that the described method is limited in its application. Thus, in the case of projecting a point to a non-rational Bézier curve, (when all the weights [w] are equal), then the coefficients a, b and c are equal to zero, and the polynomial equation transformed into the identity 0 = 0. Such a way before using the method described above should be checked for equality of weights with each other (or the vanishing of the coefficients [a],[b],[c]).

In fact, the case of projecting a point on a non-rational Bézier curve is a lot easier than projecting on a rational Bézier curve. Using similar steps, we can see that the degree of the polynomial equation of the projection points to a non-rational cubic Bézier curve is a fifth degree (rather than the tenth, as in the case of a rational curve).

Okay. For those experienced programmers who do not know why the computer was invented, I will cite the results of similar work for a non-rational Bézier curves of third order.

The equation of the non-rational cubic Bézier curve is:

Transfer the origin of the coordinates of the curve of the projected point:

Let:

And then a polynomial equation takes the form:

where:

Printable version of this post you can download here.

That's it.
Now you can enjoy the programming.

Thanks.

A bit about math and programming

Hi all of readers.

Often, programmers are faced with various mathematical problems. An example of such problems may be determining whether the choice of object to which your mouse, or sorting a list of numbers.

In most cases, available to programmers are prepared software libraries that provide various functions to facilitate the implementation of mathematical tasks.

Experienced programmers know about these libraries and use the appropriate functions provided by these libraries. But sometimes even experienced programmers will find themselves on an equal footing with inexperienced programmers, when none of the available libraries do not have the necessary functions to solve another math problem. In such cases, a paradoxical situation, when an experienced programmer can decide the outcome of which would be less effective than the decision taken by an inexperienced programmer.

Experienced programmer sits down to solve a mathematical problem as an ordinary skilled programmer. It can take one of the technologies of software development, or to create elements of the working process with the experience of architects and testers. The main mistake the experienced programmer in this situation is that to solve a mathematical problem he will try to come up not as a mathematician, but as a programmer (even if an experienced programmer).

I would like to remind all the programmers, the computer was not invented to solve mathematical problems, and to facilitate their decisions. If someone from the programmer does not know what I would like here to say that most of the algorithms that are programmed for computers that were discovered long before the invention of computers themselves. Work Chebyshev, to quickly implement the integration were open to them in the 19 st century. Work of Bernstein laid the foundations of the modern theory of splines were performed in the early 20 th century.

I'm not trying to say that in modern mathematics does not make new discoveries. Pierre Bézier and Paul de Faget de Casteljau continued development the theory of of splines in the mid of 20 th century . Carl de Boor, Edwin Catmull, Jim Clark, not only continue to develop the theory of splines, and are co-owners and animation studios creating computer graphics and animation. There are still many people who continue the development of mathematics.

But. These people do not rely on the power of modern processors. These people rely on the knowledge. Own knowledge and expertise of their predecessors. They will not allow self to assume that if some iterative algorithm implies the existence of the loop, and to exclude the probability of calculations error, just add the extra 200 iterations of this loop. Although 300 would be better. Probably better.

We have to admit that over the past few decades, the software industry is "rejuvenated". Among the students already there is a perception that programming - it's easy money. It is impossible not to agree that working at a construction site on a lot harder than to exercise the creative mind of a teenager at the time of programming. Surfing the net and not so tired as on construction sites, and moral satisfaction from showing their own creativity encouraged. Can you imagine what would have happened if the pavers brick walls of multistory buildings showed their creativity when laid another brick to the building? And with all this, the work of programmers costs not less than the work of the builders. It is obvious that in this situation as soon as the young man learned the basics of operating system it goes work to the IT-company. Getting a job, a young man begins to realize that his job is already claimed by another 5 connoisseurs of operating systems. And not to be dismissed from the company, a young man starts studying modern technology programming. Extreme Programming, Agaile, etc. Yes, this man becomes an experienced programmer, and it will not be replaced by another expert of operating systems.

It turns out that an experienced programmer is completely helpless against the objectives for which the computer was invented.

I suspect that now you want to tell me - "... the computer is intended not only for mathematical problems, and quite an experienced programmer would be useful for architectural design of client-server applications ...". And here I agree with you. Yes, an experienced programmer will use special patterns of application design. In his hands, fully justified and Extreme Programming and Agile. But. Please spend a little experiment. When you meet an experienced programmer, ask him - if he knew any planning theory of the critical path? Theory of the shortest path? Are there any known examples of problems that have no algorithmic solution? If your interlocutors know at least one of the above questions, then you're in luck. And you'll find that experienced programmers on a lot less than you thought. At the same few, how many skilled mathematicians less than people who know the multiplication table.

Thanks a lot.

Surface Reconstruction Tool for Blender3d. Version 1.2

I salute All and want to congratulate all about end of the winter and to warm spring.

And to continue the good news...

Since the first release passed one and a half months. During this time, people who seemed interesting our product, give us many valuable recommendations. We have accumulated information and return to continue the work.

And now, after six weeks of work, we're giving users a new version of Surface Reconstruction Tool.

Among the improvements that we've added a new version of Surface Reconstruction Tool includes:

1. To the library was included ability to specify the 3DM format version, where user can save the results. By default, Blender-script saves the 3DM-file is the third version of the format (instead of version 4 as it was before). This allows you to open saved 3DM-files using as application Ayam as native Rhino3d.
2. Approximation spline surfaces have become more sophisticated and effective. This will significantly reduce the volume of storage space required to represent the approximating surfaces.
3. For the new version of the library were developed, implemented and tested more sophisticated mathematical algorithms. In particular, it was identified and corrected the defect projection curves on the spline surface with a curved space of parameters, and also developed a fast and reliable analytical algorithm for projecting points on the spline curves. In general, these improvements have accelerated the algorithm several times.

As for the first version of the library, access interface to new version processed through a Python-script for the application Blender3d version 2.49. Ie to start using Surface Reconstruction Tool, Blender's users should download and install our package.

I am sure that our implementation of the library Surface Reconstruction Tool will not only interesting for its current users, but will be in demand for many new users.

We all means try to make our product useful and continue to ask all users to leave their wishes regarding the direction of its development and improvement.

For Download a latest version and more info about installation of Surface Reconstruction Tool, please go to the main post.

Thanks a lot and waiting for your feedbacks.