Projecting a point on a Bézier curve

Hi All my readers.

In this post I'd like to show how to perform the projection of a point to rational cubic Bézier curve.

In fact, this procedure may not seem very useful for everyone. In the end, is there any sense to do Bézier curves in problems of geometric programming problems? However, if someone of the readers of this post had heard about such concepts as BSpline or NURBS, I am sure that this post will show them not only interesting but useful too.

Therefore, I will ask my readers to take my word - namely, any BSpline or NURBS-curve can be converted into one (or a series) of Bézier curves. Yes, do not be surprised. It is true. Therefore, knowing how to treat the problem with Bézier curves will always have the opportunity to consider the problems associated with BSpline or NURBS curves in a similar way.

Consider the rational Bézier curve of order 3. We will talk specifically about the Bézier curve of that order.

Rational Bézier curve of order 3 define by:

Denote a point that is projected onto this curve as G;

Next, we use one of the properties of Bézier curves: namely “the transfer of all control points of a Bézier curve by the same vector does not affect the shape of the curve" and give the origin of the system coordinates of the Bézier curve to a point G.

Thus, in view of transfer of control points of the curve, then we will use the following change of variables:

Give the equation of a Bézier curve to a polynomial form:

Make the following change of:

then the equation of a Bézier curve takes the form:

Define the derivative of this equation:

After the algebraic manipulations, we obtain the following equation:

where

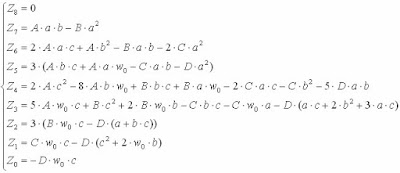
Now we can return to the equation of determining the projection of a point on a Bézier curve.
Required equation has the form:

Or:

Now we can obtain a polynomial equation, whose solution will give us the answer to the question "Where are projected onto a point on a Bézier curve?"

where:

There are many ways to solve polynomial equations. In the case of this problem I used the «Bairstow-Newton» method, which allows us to be given up to find the real and complex roots of polynomial equations. This method worked well in terms of both speed and accuracy of search results.

After receiving the results of solving polynomial equations, only one correct result from the list of solutions is necessary to choose.

To do it, consider the following factors:

1. 
   «Bairstow-Newton» method allows us to find as real as imaginary roots. Thus, the roots of polynomial equations, which contain the imaginary part, cannot be useful.
2. Since the domain of definition of a Bézier curve lies between the values [0..1], those are real roots, which are not included in this area are not correct.
3. Because of solutions of polynomial equations obtained several real roots, then choose follows the root, which corresponds to the minimum distance between a point on the Bézier curve and the projected point.
4. If resulting solutions of polynomial equations obtained several real roots, and the distance between corresponding points on the Bézier curve and the projected point are equal, then this situation should be considered as a special (exceptional). For example if the projected point on the circle from the center of this circle.
   

Also, you should noticed that the described method is limited in its application. Thus, in the case of projecting a point to a non-rational Bézier curve, (when all the weights [w] are equal), then the coefficients a, b and c are equal to zero, and the polynomial equation transformed into the identity 0 = 0. Such a way before using the method described above should be checked for equality of weights with each other (or the vanishing of the coefficients [a],[b],[c]).

In fact, the case of projecting a point on a non-rational Bézier curve is a lot easier than projecting on a rational Bézier curve. Using similar steps, we can see that the degree of the polynomial equation of the projection points to a non-rational cubic Bézier curve is a fifth degree (rather than the tenth, as in the case of a rational curve).

Okay. For those experienced programmers who do not know why the computer was invented, I will cite the results of similar work for a non-rational Bézier curves of third order.

The equation of the non-rational cubic Bézier curve is:

Transfer the origin of the coordinates of the curve of the projected point:

Let:

And then a polynomial equation takes the form:

where:

Printable version of this post you can download here.

That's it.
Now you can enjoy the programming.

Thanks.